论文: Cascade R-CNN: Delving into High Quality Object Detection - CVPR2018
作者:Zhaowei Cai, Nuno Vasconcelos
团队:UC San Diego, UC San Diego
Github - zhaoweicai/cascade-rcnn(Caffe)
Github - zhaoweicai/Detectron-Cascade-RCNN
Cascade R-CNN 关于的是如何选择最佳 IoU.
目标检测任务中,IoU(intersection over union) 阈值往往被用于定义正样本和负样本的选取. 采用低 IoU 阈值训练的目标检测器,通常会产生很多冗余检测结果,如 IoU=0.5. 而增加 IoU 阈值,会导致检测器性能下降. 分析其原因在于:
[1] - 由于正样本的指数级衰减,导致训练的过拟合(正样本被过滤,导致样本数量过少).
[2] - 由于训练时采用的 IoU 和检测的最优 IoU 的不一致性,导致 mismatch.
Cascade R-CNN 方法是采用逐渐递增的 IoU 阈值训练的序列的检测器,其序列化地选择更优的正样本和负样本. 其训练是 stage-by-stage 的.
1. 问题描述
目标检测主要解决两个任务:
[1] - 目标检测器需要解决类别识别问题,以从背景中区分前景目标,并分配给目标物体以正确的类别标签.
[2] - 目标检测器需要解决物体定位问题,以分配给不同目标物体以精确的边界框.
由于目标检测面临着许多“很接近(close)” 的负样本,其对应着“接近但并不正确(close but not correct)” 边界框,导致目标检测器必须找到正确的正样本,同时过滤这些接近的负样本.
现阶段很多目标检测器是基于 two-stage R-CNN 框架的,其是一个 multi-task 问题,同时进行物体分类和边界框识别. 训练时,一般是首先提取 region proposals,然后再对 proposals 进行分类,同时将 proposals 回归到对应的 GT boxes. 其中,由于要对 proposals 进行分类以确定类别标签,首先就要确定对哪些 proposals 进行分类. 最普遍的做法是,利用 proposals 与 GT boxes 的 IoU 来选择,如 IoU=0.5. IoU 阈值是用于定义正样本和负样本选取的必要项.
关于 IoU 阈值的选择,如下图:
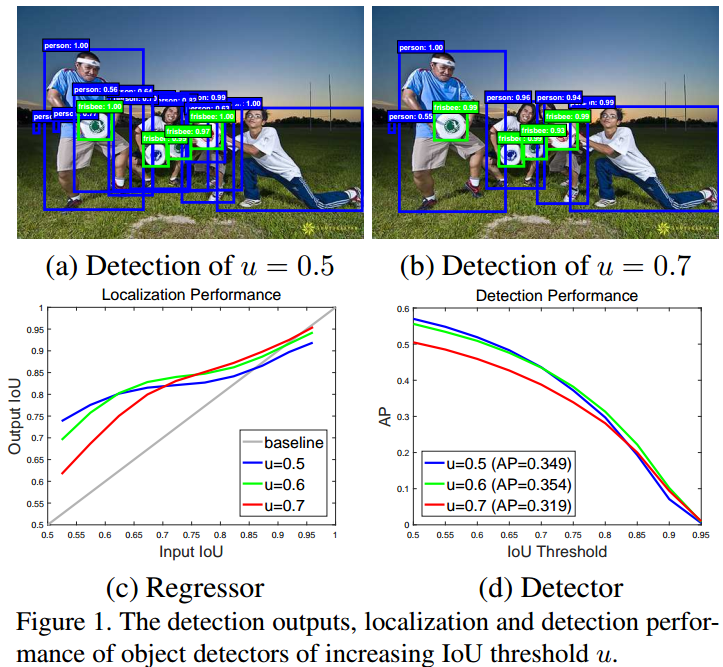
图(a)中,目标检测器常用 IoU 阈值为 0.5,其对于正样本是比较宽松的标准. 因此,结果中往往会包含很多冗余边界框. 普遍认为,接近假正样本(false positives) 一般都能通过 IoU >= 0.5 的测试. 虽然低于 IoU=0.5 阈值的样本也是丰富和多样化的,但它们会导致检测器难以有效的区分相似的假正样本(close false positives),难以进行训练.
图(b) 中,将 IoU 阈值设为 0.7,可以减少冗余检测框的数量,使检测器的输出中包含较少的接近假正样本(close false positives).
图(c) 中,横轴是 proposal boxes 与 GT boxes 的 IoU,纵轴为回归后所预测的 boxes 与 GT boxes 的 IoU,纵轴的值越大越好. 可以看出,相比于 baseline,其它的 IoU 表现都更好. IoU 越高,检测器的预测结果更好. 从该图可以看出,每个边界框回归器对于输入 IoU 与检测器训练时所采用的 IoU 阈值相接近时(设定IoU阈值的周围),性能表现最优. 目标检测器中回归器的输出 IoU 一般会优于输入 IoU,且随着 u 的增大,对于大于 IoU 阈值的 proposals 的优化效果有一定的提升作用.
图(d) 中,IoU 阈值设为 0.7 时,检测器的精度明显较低. 而在 0.5 和 0.6 时,精度相差不大,IoU=0.5 还有少许的提升. 也就是说,仅仅增大训练时所采用的 IoU 阈值是不可行的,并不能提升检测器的精度. 其原因在于:(1) IoU 阈值增大,导致正样本数量指数级减少,模型训练出现过拟合; (2) 在推断(inference)时,采用的 IoU 阈值与训练时采用的 IoU 阈值不匹配,也导致检测器精度下降.
Cascade R-CNN 的基本思想是,单一检测器只能是对单一 IoU 层次是最优的. Cascade R-CNN 考虑了对给定 IoU 阈值的优化. 即,采用级联的方式,首先利用 IoU=0.5 的网络,提升输入的 proposals;比如 IoU 提升到 0.6,再利用IoU=0.6的网络进一步的提升;比如 IoU 提升到 0.7,再利用IoU=0.7 的网络进行提升. 逐步的提升检测器的精度.
Cascade R-CNN is a multi-stage extension of the R-CNN, where detector stages deeper into the cascade are sequentially more selective against close false positives. The cascade of R-CNN stages are trained sequentially, using the output of one stage to train the next. This is motivated by the observation that the output IoU of a regressor is almost invariably better than the input IoU.
2. 目标检测
如下图:
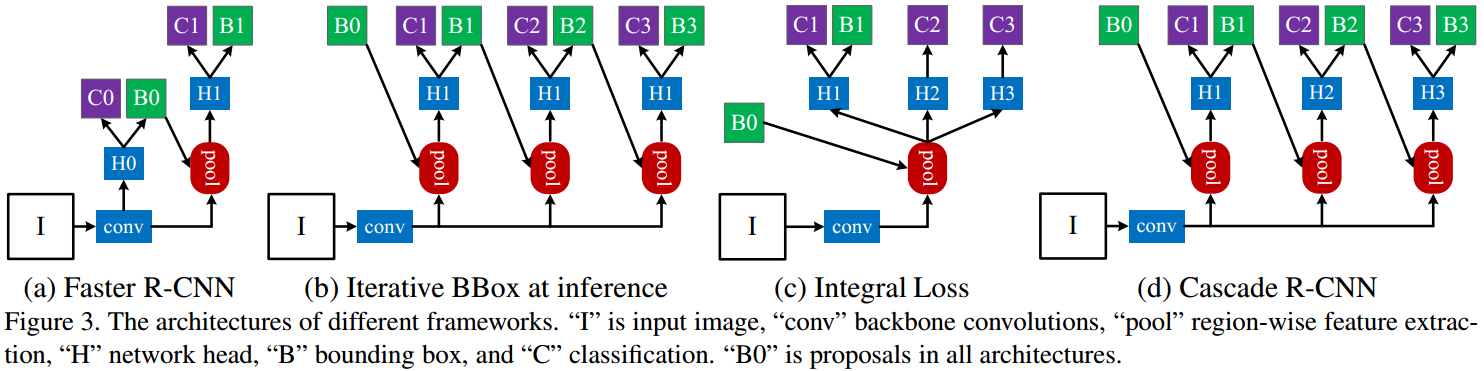
图中,对于 Faster R-CNN,
[1] - first stage,H0 为 proposal sub-network,用于对整个输入图像进行处理,输出初步的检测结果,即:object proposals. 如 RPN.
[2] - second stage,H2 为 RoI 检测 sub-network,用于对 object proposals 进行处理,记为:detection head.
[3] - final stage,C 为 classification score;B 为 bounding box,分别对应到每个 RoI 的输出.
2.1. 边界框回归
边界框 $\mathbf{b} = (b_x, b_y, b_w, b_h)$,表示了图片 $x$ 的四个坐标.
边界框回归任务旨在,采用回归器 $f(x, \mathbf{b})$ 将候选边界框 $\mathbf{b}$ 回归到目标边界框 $\mathbf{g}$.
回归器 $f(x, \mathbf{b})$ 可以描述为,基于训练样本 $\lbrace \mathbf{g}_i, \mathbf{b}_i \rbrace$,最小化边界框损失函数:
$$ \mathcal{R}_{loc}[f] = \sum_{i=1}^N L_{loc}(f(x_i, \mathbf{b}_i), \mathbf{g}_i) $$
其中,$L_{loc}$ 在 R-CNN 中采用的是 L2 损失函数,而在 Fast R-CNN 采用的是 smoothed L1 损失函数.
为了进一步增强回归器关于尺度和位置(scale vs. location)的不变性,$L_{loc}$ 是基于距离向量 $\Delta = (\delta_x, \delta_y, \delta_w, \delta_h)$ 进行的计算:
$$ \begin{cases} \delta_x = \frac{g_x - b_x}{b_w} \\ \delta_y = \frac{g_y - b_y}{b_h} \\ \delta_w = log(\frac{g_w}{b_w}) \\ \delta_h = log(\frac{g_h}{b_h}) \end{cases} $$
由于边界框回归往往是关于 $b$ 的很小的调整,计算得到的 $\delta$ 的数值可能非常小,因此,边界框损失函数的 loss 值通常比分类任务的值小. 对此,为了提升 multi-task 学习的有效性,$\Delta$ 往往采用其均值和方差进行归一化,如:
$$ \begin{cases} \delta_x' = \frac{\delta_x - \mu_x}{\sigma_x} \\ \delta_y' = \frac{\delta_y - \mu_y}{\sigma_y} \\ \delta_w' = \frac{\delta_w - \mu_w}{\sigma_w} \\ \delta_h' = \frac{\delta_h - \mu_h}{\sigma_h} \end{cases} $$
2.2. 迭代边界框回归
在 Cascade R-CNN 之前,也有研究说明了,单一回归 $f$ 处理不足以精确定位. 需要迭代的应用 $f$ 进行处理,以逐渐精细化边界框 $\mathbf{b}$:
$$ f'(x, \mathbf{b}) = f \circ f \circ ... \circ f(x, \mathbf{b}) $$
这种方法被称为:迭代边界框回归(iterative bounding box regression),记为:iterative BBox. 如Figure3(b),其所有的 head 网络是相同的.
但是,迭代边界框回归忽略了两个问题:
[1] - 如图 Figure1 中所示,采用 IoU=0.5 训练的回归器 $f$ ,其对于 IoU 更高的图像检测效果是非最优的. 实际上,对于 IoU 大于 0.85 的情况,其反而会对边界框有负影响.
[2] - 如下图 Figure2 所示,每次迭代后边界框的分布变化比较大. 尽管对于初始分布而言,回归器是最优的,但后面迭代后的可能非最优.
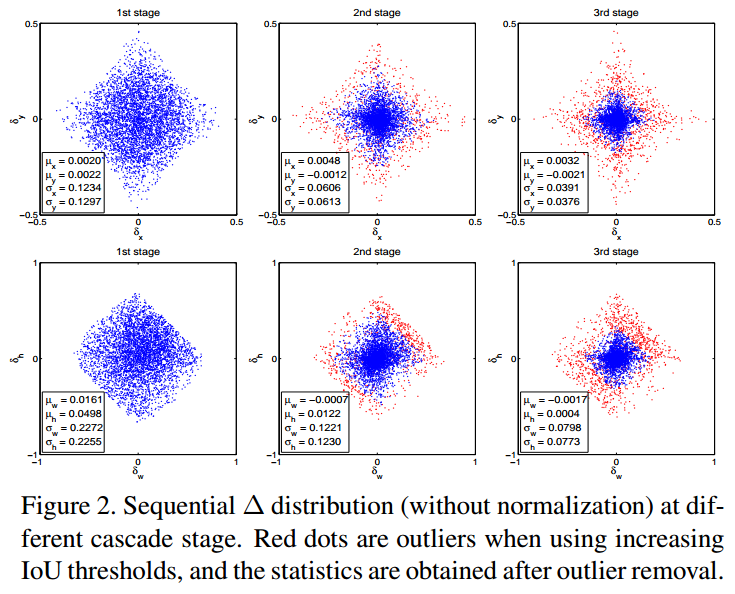
2.3. 边界框分类
分类器函数 $h(x)$ 用于从 M+1(背景+物体类别) 个类别标签中选择一个进行分配.
$h(x)$ 是 M+1 维的关于类别的后验分布估计:
$$ h_k(x) = p(y=k|x) $$
其中,$y$ 是类别标签.
给定训练数据集 $(x_i, y_i)$,分类的损失函数为:
$$ \mathcal{R}_{cls}[h] = \sum_{i=1}^N L_{cls}(h(x_i), y_i) $$
其中,$L_{cls}$ 为经典交叉熵损失函数.
2.4. 检测质量
边界框往往包含目标物体和一些背景,其很难判断检测结果是正样本还是负样本.
这个问题一般是采用 IoU 度量来解决的. 如果 IoU 大于阈值 $u$,则认为是正样本. 因此,
$$ x = \begin{cases} g_y &\text{ } IoU(x, g) \geq u \\ 0 &\text{otherwise } \end{cases} $$
其中,$g_y$ 是 GT $g$ 的类别标签. IoU 阈值 $u$ 定义了检测器的质量.
目标检测的挑战性在于,阈值等检测设置是高度对抗的. 当 IoU 阈值 $u$ 增大,则正样本数量减少,导致训练样本不足. 当 IoU 阈值 $u$ 减小,正样本的训练数据集更多更丰富,但是训练的检测器对于接近假正样本的处理能力不够. 一般来说,很难采用单个分类器能够对所有的 IoU 层级都有很好的结果.
推断阶段,由于采用 RPN 等 proposal detector 产生的大部分 proposals 都质量较低,检测器必须对于较低质量的 proposals 具有较好的判别能力.
一种直接的解决方案是,多个分类器的融合,如图 Figure3(c),在不同质量层级的优化损失函数:
$$ L_{cls}(h(x), y) = \sum_{u \in U} L_{cls}(h_u(x), y_u) $$
其中,$U$ 是 IoU 阈值集合.
这很类似于 integral loss,其 $U = \lbrace0.5, 0.55, ..., 0.75 \rbrace$,用于 COCO 竞赛的评测度量. 顾名思义,仅用于在推断阶段的分类器融合.
其难以处理的问题在于,公式(8) 中的不同损失函数对于不同数量正样本的处理.
如图 Figure4,随着 IoU 阈值 $u$ 的增加,正样本数据集减少的很快,这就会容易导致训练的过拟合.
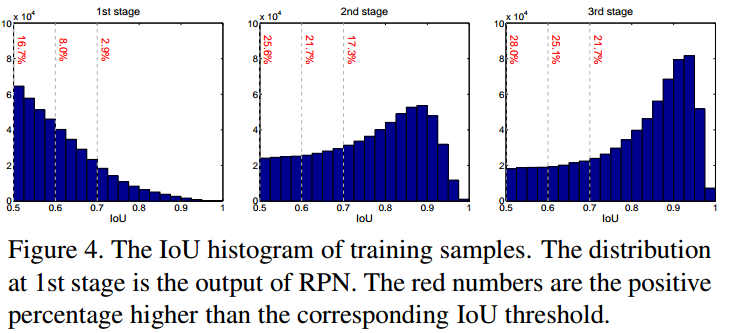
3. Cascade R-CNN
Cascade R-CNN 如图 Figure3(d).
3.1. Cascade R-CNN 的边界框回归
级联回归器:
$$ f(x, \mathbf{b}) = f_T \circ f_{T-1} \circ ... \circ f_1(x, \mathbf{b}) $$
其中,$T$ 是 cascade stages 的总数.
在同一阶段,每个回归器 $f_t$ 是关于相同的分布 $\lbrace \mathbf{b}^t \rbrace$ 进行优化的,而不是初始分布 $\lbrace \mathbf{b}^1 \rbrace$.
相比于 Figure3(b) 中的迭代边界框回归(iterative BBox) 结构,Cascade R-CNN 的区别在于:
[1] - iterative BBox 是用于提升边界框的后处理流程,而 Cascade R-CNN的回归是一种重采样流程,其会改变不同 stages 处理后的 proposals 的分布,训练时不同 stage 的输入数据分布是不同的.
[2] - Cascade R-CNN 在训练和推断是都要使用,因此不存在训练和推断间的差异性.
[3] - 回归器 $\lbrace f_T, f_{T-1}, ..., f_1 \rbrace$ 是对于不同 stages 的重采样分布(resampled distributions) 进行优化的.
3.2. Cascaded 检测
如图 Figure4 的左图所示,初始 proposals 的分布,如 RPN proposals,往往是低质量的,不可避免的会引入对于分类器的无效学习.
根据 Figure 1(c) 中所有曲线都在对角线之上的事实,如,采用特定 IoU 阈值 $u$ 训练的边界框回归器往往能够得到更高 IoU 的边界框. 对此,Cascade R-CNN 通过采用 cascade 回归作为一种重采样机制(resampling mechanism).
从样本集 $(x_i, \mathbf{b}_i)$ 开始,cascade 回归依次对更高 IoU 的样本分布 $(x_i', \mathbf{b}_i' )$ 进行重采样. 这种方式有助于保持各 stages 的正样本数据集.
对于每个 stage $t$,Cascade R-CNN 包含一个关于 IoU 阈值 $u^t$ 的分类器 $h_t$ 和回归器 $f_t$,其中,$u^t > u^{t-1}$. 最小化损失函数:
$$ L(x^t, g) = L_{cls}(h_t(x^t), y^t) + \lambda[y^t \geq 1]L_{loc}(f_t(x^t, \mathbf{b}^t), \mathbf{g}) $$
其中,$\mathbf{b}^t = f_{t-1}(x^{t-1}, \mathbf{b}^{t-1})$. $g$ 为 $x^t$ 的 GT. $\lambda=1$ 为惩罚系数. $[\cdot]$ 表示指示器函数. $y^t$ 是给定 $u^t$ 的 $x^t$ 的类别标签,由公式(7) 计算得到.
## 4. Results
4.1. 实现细节
Cascade R-CNN 的所有 cascade detection stages 具有相同的结构,即 baseline detection network 的 head 网络.
Cascade R-CNn 包含 4 个 stages,第一个 stage 用于 RPN,其它三个 stages 采用的 IoU 阈值为 $U = \lbrace 0.5, 0.6, 0.7 \rbrace$.
数据增强只有水平图片翻转.
推断阶段仅采用单一图片尺度.
4.2. 论文结果

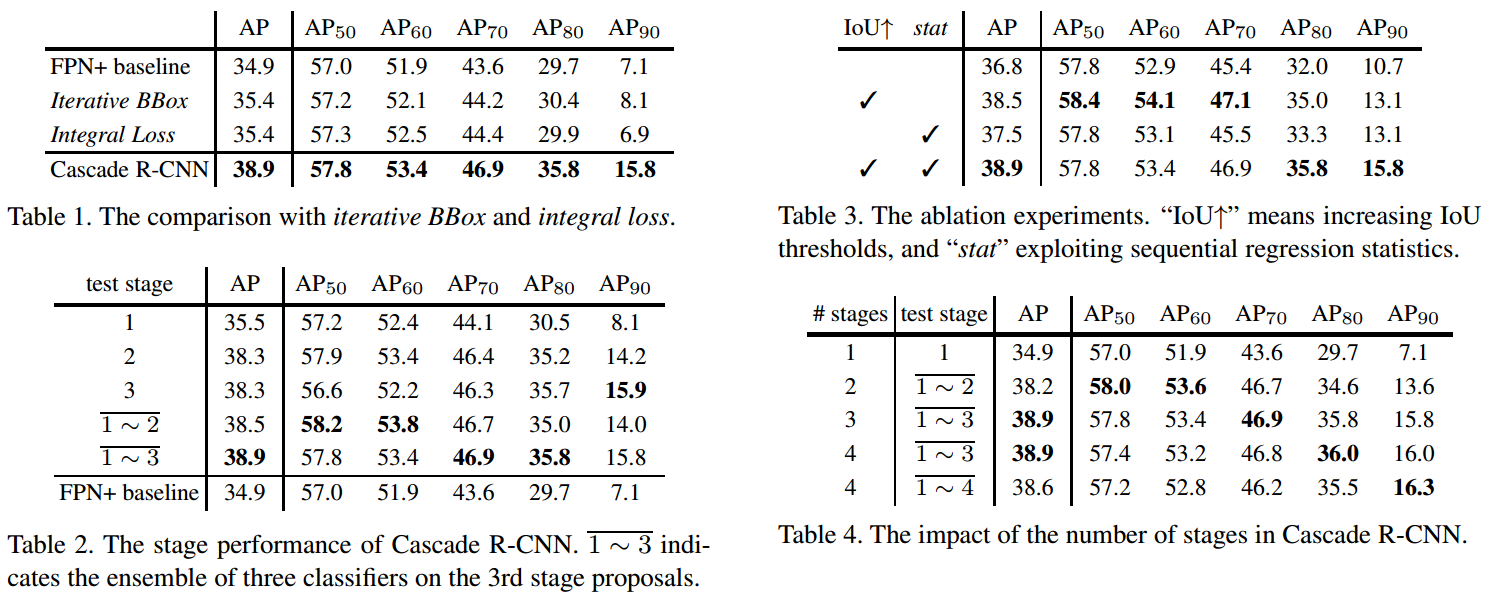
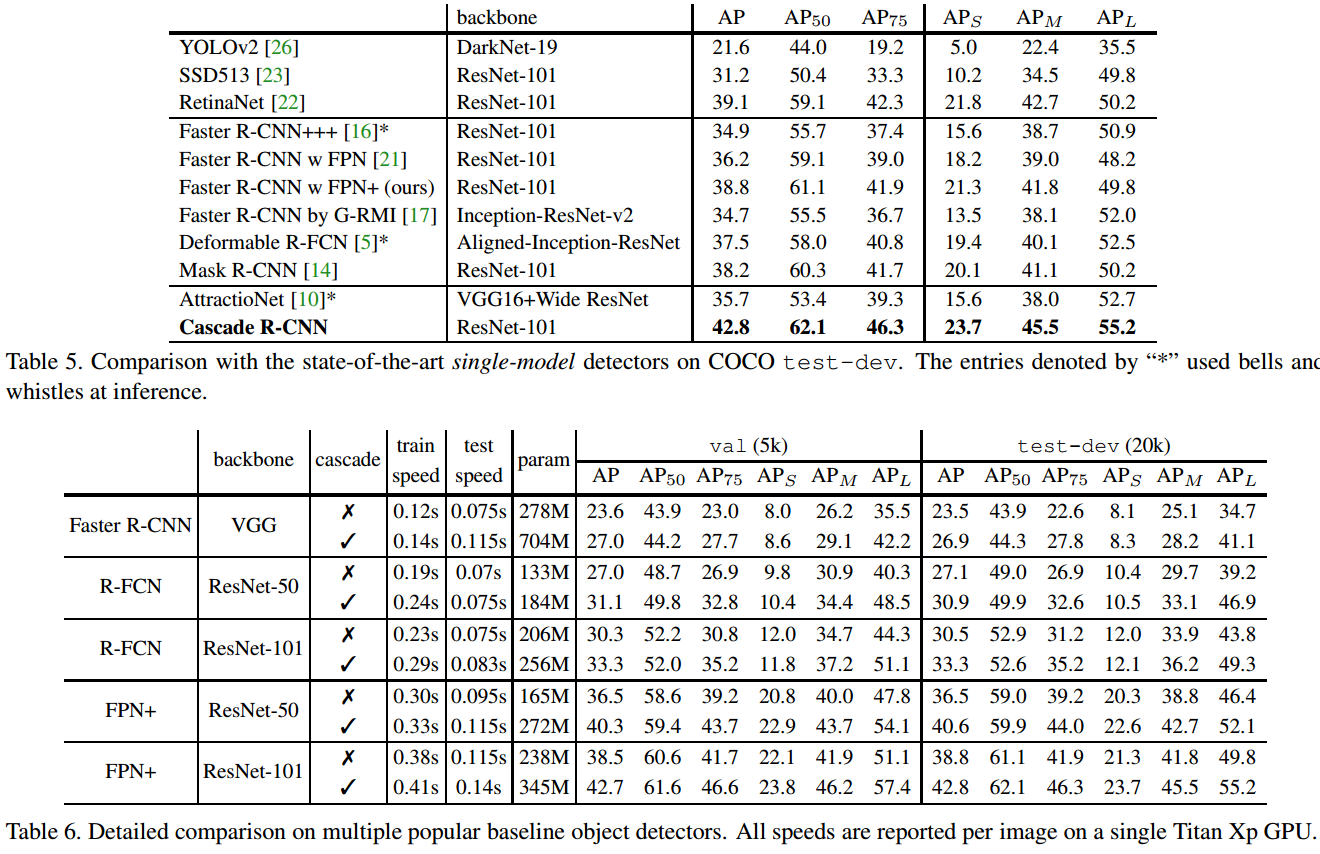
5. 相关
[1] - 目标检测-Cascade R-CNN-论文笔记
[2] - Cascade R-CNN: Delving into High Quality Object Detection
[3] - Cascade R-CNN: Delving into High Quality Object Detection - 知乎